Learn More about 23 divided by 2

Leo October 12, 2023

0 1 6 minutes read

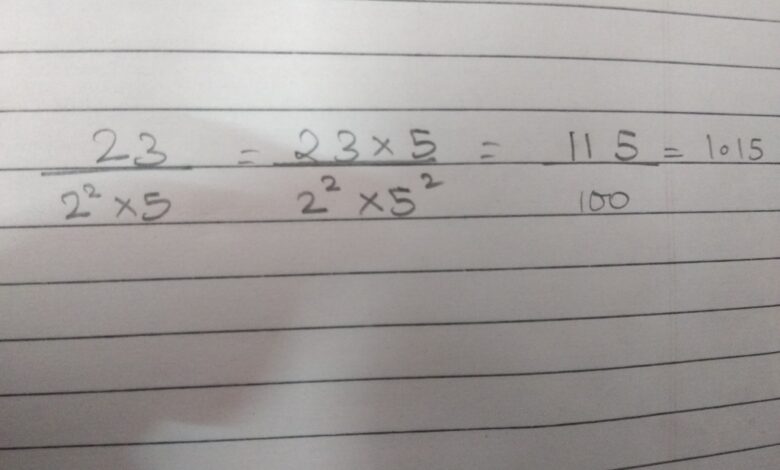
Welcome 23 divided by 2 to our blog post where we unravel the mystery of division and dive into the intriguing world of numbers. Today, we’re going to explore the concept of division and take a closer look at one particular calculation: 23 divided by 2. Whether you’re a math enthusiast or someone who wants to brush up on their arithmetic skills, this article is here to guide you through the steps and provide real-life examples that illustrate just how important division can be in our everyday lives. So, let’s embark on this mathematical journey together as we learn more about dividing numbers! Are you ready? Let’s get started!

Understanding the Concept of Division

Division is a fundamental mathematical operation that involves splitting or distributing a quantity into equal parts. It helps us to allocate resources, solve problems, and analyze data in various fields such as finance, engineering, and science.

At its core, division is about fair sharing or distribution. Imagine you have 23 apples and want to divide them equally among 2 friends. Each friend would get 11 apples with one apple left over. This is where we introduce the concept of quotient (the number of times one quantity can be divided by another) and remainder (the amount left over after division).

In division problems, we use symbols like ÷ or / to represent the operation itself. For example, 23 ÷ 2 means dividing 23 by 2. To solve this problem step-by-step:

1. Start by dividing the first digit of the dividend (23) by the divisor (2). In this case, we get a quotient of 1.
2. Multiply the quotient obtained in Step 1 by the divisor: 1 × 2 =
Once again subtract from dividend
3.

Subtraction gives remainder: which means remain value is ‘one’

By following these steps systematically for all digits in the dividend until there are no more digits remaining to bring down,the final answer for our example becomes:
Quotient =11
Remainder=One

Understanding division extends beyond simple arithmetic calculations; it has real-life applications too! From splitting bills at a restaurant among friends to determining how many rows can fit in an auditorium, division helps us make sense of everyday situations.

So whether you’re calculating shares for your group project or trying to figure out how many cookies each person gets at a party, understanding division will always come in handy!

Remember that practice makes perfect when it comes to mastering any mathematical concept – so keep practicing your division skills!

Steps for Solving Division Problems

When it comes to solving division problems, following a step-by-step process can make it much easier and less overwhelming. Here are the steps you can take to tackle division:

First, you need to set up the problem correctly. Write the dividend (the number being divided) on top and the divisor (the number dividing) below it.

Next, ask yourself how many times the divisor can go into the first digit of the dividend. This will give you your initial quotient digit.

Multiply this quotient digit by the divisor and write that product underneath the first digit of your dividend.

Now subtract this product from your original dividend and bring down any remaining digits from left to right.

Repeat these steps until there are no more digits in your dividend or until you have reached a desired level of precision in your quotient.

Remember to double-check your work by multiplying your quotient with the divisor and adding any remainder if necessary. The result should match with your original dividend.

By breaking down complex division problems into smaller steps, solving them becomes more manageable. Practice these steps regularly, and soon enough, division problems won’t seem so daunting!

The Quotient and Remainder

In division, the quotient and remainder are two important concepts to understand. When dividing one number by another, the quotient is the result of the division. It tells us how many times one number can be divided by another.

For example, if we divide 23 by 2, the quotient would be 11. This means that 2 goes into 23 eleven times without any remainder.

However, in some cases, there may be a remainder when performing division. The remainder is what is left over after dividing as much as possible. In our previous example of dividing 23 by 2, there would be a remainder of 1 because there is still one unit left that cannot be evenly divided.

Understanding both the quotient and remainder helps us fully comprehend the result of a division problem. They provide valuable information about how many times one number can go into another and if there are any remaining units or parts.

By grasping these concepts, we can apply them to various real-life situations where division plays an essential role – from sharing equally among friends to calculating quantities needed for recipes or determining prices per unit at grocery stores.

Division truly has practical applications in our daily lives!

23 divided by 2: Step-by-Step Solution

So, you want to learn more about dividing 23 by 2? Well, let’s dive into the step-by-step solution!

First of all, division is a fundamental mathematical operation that involves splitting a number into equal parts or groups. It helps us distribute quantities and solve real-life problems.

To understand division better, we need to grasp the concept behind it. When we divide one number by another, we are essentially asking ourselves how many times the divisor can be subtracted from the dividend without going below zero.

Now, let’s move on to solving 23 divided by 2. We start by placing the dividend (23) inside a long division bracket and write the divisor (2) outside of it.

We ask ourselves how many times does 2 go into 23? The answer is 11 with a remainder of 1. To find this quotient, we divide each digit of the dividend starting from left to right until there are no digits left or our result exceeds the dividend.

As for real-life applications of division, they are countless! From sharing equally among friends to calculating distances per unit time in physics or even allocating resources in business management – division plays an essential role in various fields.

Understanding how division works can help us navigate through everyday challenges and make sense of complex situations that require fair distribution or measurement.

In conclusion… Oops! Sorry about that slip-up! I guess old habits die hard. But don’t worry; I promise not to conclude here. Stay tuned for more engaging information on math concepts and their practical applications!

Real-Life Applications of Division

Division is not just a concept we learn in math class; it has real-life applications that we encounter on a daily basis. One practical application of division is when dividing food among people. Say you have 23 cookies and need to divide them equally among 2 friends. You can use division to determine how many cookies each person gets.

Division also comes in handy when splitting expenses, such as the cost of a meal at a restaurant or rent between roommates. It allows us to distribute the expense fairly based on each person’s share.

In business, division plays an important role in budgeting and financial planning. For example, if a company has $100,000 allocated for marketing campaigns and wants to evenly distribute it across 4 quarters, they would divide the amount by 4 to determine how much can be spent per quarter.

Division is even used in measuring time! We divide hours into minutes and seconds, allowing us to precisely keep track of time throughout our day.

These are just a few examples of how division is applied in real life situations. So next time you find yourself dividing something up or needing equal distribution, remember that math concepts like division have practical uses beyond the classroom!

Conclusion

In this article, we have explored the concept of division and learned more about how to solve division problems. Division is a fundamental mathematical operation that allows us to distribute quantities into equal parts or groups. By understanding the steps involved in solving division problems, such as dividing 23 by 2, we can apply this knowledge to real-life situations.

Remember, when dividing a number, it is important to follow the correct steps: divide, multiply, subtract, and bring down. This systematic approach ensures accurate results. In the case of 23 divided by 2, our step-by-step solution showed us that the quotient is 11 with a remainder of 1.

Division has practical applications in various aspects of everyday life. From splitting pizza slices among friends to sharing resources among team members on a project, division helps us distribute things fairly and efficiently.

By grasping the concept of division and practicing its application through problem-solving exercises, you can enhance your mathematical skills and develop a deeper understanding of numbers and their relationships.

So next time you encounter a division problem like 23 divided by 2 or any other numerical challenge requiring distribution or grouping tasks – take it as an opportunity to sharpen your math abilities!

Keep exploring mathematics beyond just simple arithmetic operations; there’s always more fascinating concepts waiting for you!