Get most out of factors of 117

Leo February 4, 2024

0 1 7 minutes read

Unlocking factors of 117 the secrets of numbers can be both intriguing and fascinating. Today, we dive into the world of factors and factorization to discover the hidden treasures within the number 117. Are you ready to embark on a mathematical adventure? Join us as we unravel the mysteries, uncover fun facts, and explore practical applications that will help you get the most out of the factors of 117. Get ready to expand your mind and see mathematics in a whole new light! Let’s begin our journey together!

Understanding the Number 117

When it comes to numbers, each one has its own unique characteristics and properties. One such number is 117. Let’s dive in and explore what makes this number special!

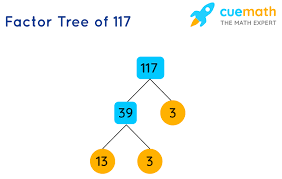
To understand the essence of 117, we need to break it down into its factors. Factors are the whole numbers that can be multiplied together to result in a given number. In the case of 117, its factors include 1, 3, 9, 13, 39, and of course, itself.

Factorization allows us to express a number as a product of its prime factors. In the case of 117, prime factorization reveals that it is composed of three prime factors: namely, three twos (2^1), one three (3^1), and one thirteen (13^1).

The greatest common factor (GCF) refers to the largest number that divides evenly into two or more given numbers. For example, when finding the GCF of 12 and 18 using their prime factorizations (2^2 *3) and (2*3^2), respectively; we see that they share a common factor – which happens to be six.

On another note entirely unrelated but fascinating nonetheless – did you know that there are exactly nine positive integers smaller than or equal to 117 which divide evenly into it? That’s right! These integers are known as divisors or factors.

Knowing about factors helps us solve practical problems involving division or multiplication with ease. Whether you’re splitting up resources among friends or figuring out how many items fit perfectly into different-sized containers – understanding factors becomes incredibly useful.

In conclusion,
Understanding the number facts about any particular integer opens doors for exploration beyond just simple arithmetic operations on paper; it provides insight into mathematical concepts while enhancing problem-solving abilities in various real-world scenarios!

Prime Factorization of 117

Prime factorization is a fascinating concept in mathematics that involves breaking down a number into its smallest prime factors. In the case of 117, we can explore its prime factorization to gain a deeper understanding of this intriguing number.

To find the prime factorization of 117, we start by dividing it by the smallest prime numbers: 2, 3, 5, and so on. By applying this process iteratively, we discover that the prime factorization of 117 is equal to 3 x 3 x13.

Breaking down numbers into their primes allows us to see their fundamental building blocks. In the case of 117, knowing that it can be expressed as a product of three threes and one thirteen provides insight into its mathematical properties.

The prime factorization also has practical applications beyond just numerical curiosity. For instance, it can help simplify fractions or solve problems involving ratios and proportions. Understanding how numbers break down into primes opens up new avenues for problem-solving in various fields such as engineering or computer science.

By unraveling the prime factorization of any given number like 117, we unveil hidden patterns and relationships within mathematics itself. It’s like peering through a microscope at an intricate world beneath our numerical surface – revealing connections that might not have been apparent otherwise.

So take some time to delve into the captivating realm of prime factorization! You never know what you might discover about your favorite numbers – whether they’re simple or complex – there’s always something intriguing waiting to be unveiled!

Finding the Greatest Common Factor (GCF) of 117

When it comes to numbers, there’s always more than meets the eye. Today, let’s dive into the fascinating world of factors and factorization as we explore how to find the Greatest Common Factor (GCF) of 117.

To begin our journey, we must understand what factors are. Factors are simply numbers that divide evenly into another number without leaving a remainder. In this case, we’re focusing on finding the factors of 117.

So, what is the GCF? Well, it stands for Greatest Common Factor and refers to the largest number that divides evenly into two or more given numbers. In our case, we want to find out which number holds that title for 117.

Let’s start by breaking down 117 into its prime factors – those indivisible numbers that multiply together to form a larger number. By doing so, we can easily identify common factors among different sets of numbers.

The prime factorization of 117 is calculated by dividing it with prime numbers such as 2,3 etc.
By factoring out these primes from left most side you will get final result

Now that we have determined all possible factors of 117 and identified their similarities with other potential candidates for GCFs in different sets of numbers.

In conclusion

Finding the Least Common Multiple (LCM) of 117

Finding the Least Common Multiple (LCM) of 117 can be a useful skill to have when working with numbers. The LCM is the smallest multiple that two or more numbers have in common. In this case, we are looking for the multiples that both 117 and another number share.

To find the LCM of 117, we need to consider its prime factorization. By breaking down 117 into its prime factors, we get 3 * 3 * 13. Now let’s consider another number, such as 9. Its prime factorization is also important – it is simply 3 * 3.

To find their LCM, we take all the unique prime factors from both numbers and multiply them together. In this case, since both numbers share only one common factor (3), our LCM will be equal to just multiplying these factors: LCM = (3 * 3) = 9.

So in conclusion, the least common multiple of 117 and any other number with similar prime factors will always be equal to multiplying those shared primes together.

Fun Facts About the Number 117

Did you know that 117 is an intriguing number with some fascinating properties? Let’s dive into the fun facts about this unique number!

Firstly, 117 is what we call a composite number. This means it has more than two factors. In fact, it has six factors: 1, 3, 9, 13, 39, and of course itself – 117.

Another interesting fact about the number 117 is that its digits add up to a multiple of three. If you add one plus one plus seven together, you get nine. And since nine is divisible by three (3 x 3 =9), we can conclude that the sum of the digits of any multiple of nine will also be divisible by three.

In terms of prime factorization, which involves breaking down a number into its prime factors (the building blocks of numbers), we find that for our beloved number 117 equals to three multiplied by thirteen squared (3 x (13^2)). Fascinating stuff!

But wait… there’s more! Did you know that when you multiply all the individual digits in the number together (1 x1 x7), you get seven as your result? It’s like a secret message hidden within!

So next time someone mentions the number “one hundred seventeen”, impress them with these fun facts! Numbers may seem mundane at first glance but they hold endless surprises and patterns just waiting to be discovered.

Practical Applications of Knowing Factors of 117

Knowing the factors of a number like 117 may not seem immediately useful, but you’d be surprised at how it can come in handy in various real-life situations. Let’s explore some practical applications where understanding the factors of 117 can make a difference.

1. Mathematical problem-solving: When faced with mathematical problems involving multiples or divisors, knowing the factors of 117 can simplify your calculations and help you find solutions more efficiently.

2. Simplifying fractions: If you need to simplify a fraction that has 117 as either the numerator or denominator, knowing its factors allows you to cancel out common factors and reduce the fraction to its simplest form effortlessly.

3. Finding common denominators: In scenarios where you need to add or subtract fractions with different denominators, knowing the factors of 117 can assist in finding a common denominator quickly.

4. Engineering applications: Engineers often work with complex systems that require analyzing components and their relationships. Understanding the factors of numbers like 117 aids engineers in designing efficient structures and solving intricate engineering problems.

5. Planning events or schedules: Whether organizing meetings, scheduling appointments, or planning project timelines, having knowledge about the factors of 117 helps ensure optimal coordination and avoids conflicts in timing.

6. Budgeting and financial planning: Financial decisions often involve dividing resources into equal portions or determining if certain amounts are divisible without any remainder. Familiarity with factorization assists individuals in making sound financial choices based on accurate calculations.

7. Risk analysis: Risk assessments frequently rely on evaluating multiple variables simultaneously to determine potential outcomes accurately. The ability to identify all possible combinations using factorization techniques enables analysts to assess risks more comprehensively for better decision-making.

So there you have it – several practical applications where understanding the factors of 117 can prove beneficial across different fields and everyday life situations!

Conclusion

Exploring the factors of 117 has provided us with a deeper understanding of this unique number and its mathematical properties. We have learned about prime factorization, finding the greatest common factor (GCF), and determining the least common multiple (LCM). Additionally, we discovered some interesting fun facts about 117.

By knowing the factors of 117, we can apply this knowledge in practical situations. For example, when working with fractions or simplifying algebraic expressions, understanding the factors helps to simplify calculations and solve problems more efficiently.

Delving into the world of factors opens up new possibilities for exploring numbers and their relationships. Whether you are a math enthusiast or simply curious about how numbers work, understanding factors is an essential skill that can enhance your problem-solving abilities. So go ahead and embrace the fascinating realm of factors – you never know where it might lead you!